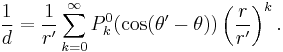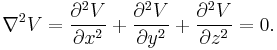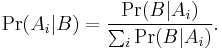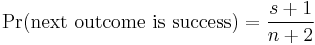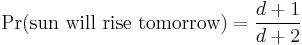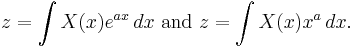Pierre-Simon Laplace

Pierre-Simon, marquis de Laplace

Pierre-Simon Laplace (1749–1827). Posthumous portrait by Madame Feytaud, 1842
Born 23 March 1749
Beaumont-en-Auge, Normandy, France
Died 5 March 1827(1827-03-05) (aged 77)
Paris, France
Nationality  France
Fields Astronomer and Mathematician
Institutions École Militaire (1769–1776)
Alma mater University of Caen
Academic advisors Jean d'Alembert
Christophe Gadbled
Pierre Le Canu
Doctoral students Siméon Denis Poisson
Known for Work in Celestial Mechanics
Laplace's equation
Laplacian
Laplace transform
Laplace distribution
Laplace's demon
Laplace expansion
Young–Laplace equation
Laplace number
Laplace limit
Laplace invariant
Laplace principle
Signature

Pierre-Simon, marquis de Laplace (/ləˈplɑːs/; 23 March 1749 – 5 March 1827) was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste (Celestial Mechanics) (1799–1825). This work translated the geometric study of classical mechanics to one based on calculus, opening up a broader range of problems. In statistics, the so-called Bayesian interpretation of probability was mainly developed by Laplace.[1]

He formulated Laplace's equation, and pioneered the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplacian differential operator, widely used in mathematics, is also named after him.

He restated and developed the nebular hypothesis of the origin of the solar system and was one of the first scientists to postulate the existence of black holes and the notion of gravitational collapse.

He is remembered as one of the greatest scientists of all time, sometimes referred to as a French Newton or Newton of France, with a phenomenal natural mathematical faculty superior to any of his contemporaries.[2]

He became a count of the First French Empire in 1806 and was named a marquis in 1817, after the Bourbon Restoration.

Contents

Early life

Many details of the life of Laplace were lost when the family château burned in 1925.[3] Laplace was born in Beaumont-en-Auge, Normandy in 1749. According to W. W. Rouse Ball (A Short Account of the History of Mathematics, 4th edition, 1908), he was the son of a small cottager or perhaps a farm-labourer, and owed his education to the interest excited in some wealthy neighbours by his abilities and engaging presence. Very little is known of his early years. It would seem from a pupil he became an usher in the school at Beaumont; but, having procured a letter of introduction to d'Alembert, he went to Paris to push his fortune. However, Karl Pearson[3] is scathing about the accuracies in Rouse Ball's account and states,

Indeed Caen was probably in Laplace's day the most intellectually active of all the towns of Normandy. It was here that Laplace was educated and was provisionally a professor. It was here he wrote his first paper published in the Mélanges of the Royal Society of Turin, Tome iv. 1766–1769, at least two years before he went at 22 or 23 to Paris in 1771. Thus before he was 20 he was in touch with Lagrange in Turin. He did not go to Paris a raw self-taught country lad with only a peasant background! In 1765 at the age of sixteen Laplace left the "School of the Duke of Orleans" in Beaumont and went to the University of Caen, where he appears to have studied for five years. The 'École Militaire' of Beaumont did not replace the old school until 1776.

His parents were from comfortable families. His father was Pierre Laplace, and his mother was Marie-Anne Sochon. The Laplace family was involved in agriculture until at least 1750, but Pierre Laplace senior was also a cider merchant and syndic of the town of Beaumont.

Pierre Simon Laplace attended a school in the village run at a Benedictine priory, his father intending that he would be ordained in the Roman Catholic Church, and at sixteen he was sent to further his father's intention at the University of Caen, reading theology.[4]

At the university, he was mentored by two enthusiastic teachers of mathematics, Christophe Gadbled and Pierre Le Canu, who awoke his zeal for the subject. Laplace did not graduate in theology but left for Paris with a letter of introduction from Le Canu to Jean le Rond d'Alembert.[4]

According to his great-great-grandson,[3] d'Alembert received him rather poorly, and to get rid of him gave him a thick mathematics book, saying to come back when he had read it. When Laplace came back a few days later, d'Alembert was even less friendly and did not hide his opinion that it was impossible that Laplace could have read and understood the book. But upon questioning him, he realized that it was true, and from that time he took Laplace under his care.

Another version is that Laplace solved overnight a problem that d'Alembert set him for submission the following week, then solved a harder problem the following night. D'Alembert was impressed and recommended him for a teaching place in the École Militaire.[5]

With a secure income and undemanding teaching, Laplace now threw himself into original research and, in the next seventeen years, 1771–1787, he produced much of his original work in astronomy.[6]

Laplace further impressed the Marquis de Condorcet, and even in 1771 Laplace felt that he was entitled to membership in the French Academy of Sciences. However, in that year, admission went to Alexandre-Théophile Vandermonde and in 1772 to Jacques Antoine Joseph Cousin. Laplace was disgruntled, and at the beginning of 1773, d'Alembert wrote to Lagrange in Berlin to ask if a position could be found for Laplace there. However, Condorcet became permanent secretary of the Académie in February and Laplace was elected associate member on 31 March, at age 24.[7]

He married Marie-Charlotte de Courty de Romanges in his late thirties and the couple had a daughter, Sophie, and a son, Charles-Émile (b. 1789).[3][8]

Analysis, probability and astronomical stability

Laplace's early published work in 1771 started with differential equations and finite differences but he was already starting to think about the mathematical and philosophical concepts of probability and statistics.[9] However, before his election to the Académie in 1773, he had already drafted two papers that would establish his reputation. The first, Mémoire sur la probabilité des causes par les événements was ultimately published in 1774 while the second paper, published in 1776, further elaborated his statistical thinking and also began his systematic work on celestial mechanics and the stability of the solar system. The two disciplines would always be interlinked in his mind. "Laplace took probability as an instrument for repairing defects in knowledge."[10] Laplace's work on probability and statistics is discussed below with his mature work on the Analytic theory of probabilities.

Stability of the solar system

Sir Isaac Newton had published his Philosophiae Naturalis Principia Mathematica in 1687 in which he gave a derivation of Kepler's laws, which describe the motion of the planets, from his laws of motion and his law of universal gravitation. However, though Newton had privately developed the methods of calculus, all his published work used cumbersome geometric reasoning, unsuitable to account for the more subtle higher-order effects of interactions between the planets. Newton himself had doubted the possibility of a mathematical solution to the whole, even concluding that periodic divine intervention was necessary to guarantee the stability of the solar system. Dispensing with the hypothesis of divine intervention would be a major activity of Laplace's scientific life.[11] It is now generally regarded that Laplace's methods on their own, though vital to the development of the theory, are not sufficiently precise to demonstrate the stability of the Solar System,[12] and indeed, the Solar System is now understood to be chaotic, although it actually appears to be fairly stable.

One particular problem from observational astronomy was the apparent instability whereby Jupiter's orbit appeared to be shrinking while that of Saturn was expanding. The problem had been tackled by Leonhard Euler in 1748 and Joseph Louis Lagrange in 1763 but without success.[13] In 1776, Laplace published a memoir in which he first explored the possible influences of a purported luminiferous ether or of a law of gravitation that did not act instantaneously. He ultimately returned to an intellectual investment in Newtonian gravity.[14] Euler and Lagrange had made a practical approximation by ignoring small terms in the equations of motion. Laplace noted that though the terms themselves were small, when integrated over time they could become important. Laplace carried his analysis into the higher-order terms, up to and including the cubic. Using this more exact analysis, Laplace concluded that any two planets and the sun must be in mutual equilibrium and thereby launched his work on the stability of the solar system.[15] Gerald James Whitrow described the achievement as "the most important advance in physical astronomy since Newton".[11]

Laplace had a wide knowledge of all sciences and dominated all discussions in the Académie.[16] Laplace seems to have regarded analysis merely as a means of attacking physical problems, though the ability with which he invented the necessary analysis is almost phenomenal. As long as his results were true he took but little trouble to explain the steps by which he arrived at them; he never studied elegance or symmetry in his processes, and it was sufficient for him if he could by any means solve the particular question he was discussing.[6]

On the figure of the Earth

During the years 1784–1787 he published some memoirs of exceptional power. Prominent among these is one read in 1783, reprinted as Part II of Théorie du Mouvement et de la figure elliptique des planètes in 1784, and in the third volume of the Mécanique céleste. In this work, Laplace completely determined the attraction of a spheroid on a particle outside it. This is memorable for the introduction into analysis of spherical harmonics or Laplace's coefficients, and also for the development of the use of what we would now call the gravitational potential in celestial mechanics.

Spherical harmonics

In 1783, in a paper sent to the Académie, Adrien-Marie Legendre had introduced what are now known as associated Legendre functions.[6] If two points in a plane have polar co-ordinates (r, θ) and (r ', θ'), where r ' ≥ r, then, by elementary manipulation, the reciprocal of the distance between the points, d, can be written as:

\frac{1}{d} = \frac{1}{r'} \left [ 1 - 2 \cos (\theta' - \theta) \frac{r}{r'} %2B \left ( \frac{r}{r'} \right ) ^2 \right ] ^{- \tfrac{1}{2}}.

This expression can be expanded in powers of r/r ' using Newton's generalised binomial theorem to give:

\frac{1}{d} = \frac{1}{r'} \sum_{k=0}^\infty P^0_k ( \cos ( \theta' - \theta ) ) \left ( \frac{r}{r'} \right ) ^k.

The sequence of functions P0k(cosф) is the set of so-called "associated Legendre functions" and their usefulness arises from the fact that every function of the points on a circle can be expanded as a series of them.[6]

Laplace, with scant regard for credit to Legendre, made the non-trivial extension of the result to three dimensions to yield a more general set of functions, the spherical harmonics or Laplace coefficients. The latter term is not in common use now .[6]

Potential theory

This paper is also remarkable for the development of the idea of the scalar potential.[6] The gravitational force acting on a body is, in modern language, a vector, having magnitude and direction. A potential function is a scalar function that defines how the vectors will behave. A scalar function is computationally and conceptually easier to deal with than a vector function.

Alexis Clairaut had first suggested the idea in 1743 while working on a similar problem though he was using Newtonian-type geometric reasoning. Laplace described Clairaut's work as being "in the class of the most beautiful mathematical productions".[17] However, Rouse Ball alleges that the idea "was appropriated from Joseph Louis Lagrange, who had used it in his memoirs of 1773, 1777 and 1780".[6] The term "potential" itself was due to Daniel Bernoulli, who introduced it in his 1738 memoire Hydrodynamica. However, according to Rouse Ball, the term "potential function" was not actually used (to refer to a function V of the coordinates of space in Laplace's sense) until George Green's 1828 An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism.[18][19]

Laplace applied the language of calculus to the potential function and showed that it always satisfies the differential equation:[6]

\nabla^2V={\partial^2V\over \partial x^2 } %2B {\partial^2V\over \partial y^2 } %2B {\partial^2V\over \partial z^2 } = 0.

An analogous result for the velocity potential of a fluid had been obtained some years previously by Leonard Euler.[20][21]

Laplace's subsequent work on gravitational attraction was based on this result. The quantity ∇2V has been termed the concentration of V and its value at any point indicates the "excess" of the value of V there over its mean value in the neighbourhood of the point. Laplace's equation, a special case of Poisson's equation, appears ubiquitously in mathematical physics. The concept of a potential occurs in fluid dynamics, electromagnetism and other areas. Rouse Ball speculated that it might be seen as "the outward sign" of one the "prior forms" in Kant's theory of perception.[6]

The spherical harmonics turn out to be critical to practical solutions of Laplace's equation. Laplace's equation in spherical coordinates, such as are used for mapping the sky, can be simplified, using the method of separation of variables into a radial part, depending solely on distance from the centre point, and an angular or spherical part. The solution to the spherical part of the equation can be expressed as a series of Laplace's spherical harmonics, simplifying practical computation.

Planetary and lunar inequalities

Jupiter–Saturn great inequality

Laplace presented a memoir on planetary inequalities in three sections, in 1784, 1785, and 1786. This dealt mainly with the identification and explanation of the perturbations now known as the "great Jupiter–Saturn inequality". Laplace solved a longstanding problem in the study and prediction of the movements of these planets. He showed by general considerations, first, that the mutual action of two planets could never cause large changes in the eccentricities and inclinations of their orbits; but then, even more importantly, that peculiarities arose in the Jupiter–Saturn system because of the near approach to commensurability of the mean motions of Jupiter and Saturn. (Commensurability, in this context, means related by ratios of small whole numbers. Two periods of Saturn's orbit around the Sun almost equal five of Jupiter's. The corresponding difference between multiples of the mean motions, (2nJ − 5nS), corresponds to a period of nearly 900 years, and it occurs as a small divisor in the integration of a very small perturbing force with this same period. As a result, the integrated perturbations with this period are disproportionately large, about 0.8° degrees of arc in orbital longitude for Saturn and about 0.3° for Jupiter.) Further developments of these theorems on planetary motion were given in his two memoirs of 1788 and 1789, but with the aid of Laplace's discoveries, the tables of the motions of Jupiter and Saturn could at last be made much more accurate. It was on the basis of Laplace's theory that Delambre computed his astronomical tables.[6]

Lunar inequalities

Laplace also produced an analytical solution (as it turned out later, a partial solution), to a significant problem regarding the motion of the Moon. Edmond Halley had been the first to suggest, in 1695,[22] that the mean motion of the Moon was apparently getting faster, by comparison with ancient eclipse observations, but he gave no data. (It was not yet known in Halley's or Laplace's times that what is actually occurring includes a slowing-down of the Earth's rate of rotation: see also Ephemeris time - History. When measured as a function of mean solar time rather than uniform time, the effect appears as a positive acceleration.) In 1749 Richard Dunthorne confirmed Halley's suspicion after re-examining ancient records, and produced the first quantitative estimate for the size of this apparent effect:[23] a centurial rate of +10" (arcseconds) in lunar longitude (a surprisingly good result for its time, not far different from values assessed later, e.g. in 1786 by de Lalande,[24] and to compare with values from about 10" to nearly 13" being derived about century later.)[25][26] The effect became known as the secular acceleration of the Moon, but until Laplace, its cause remained unknown.

Laplace gave an explanation of the effect in 1787, showing how an acceleration arises from changes (a secular reduction) in the eccentricity of the Earth's orbit, which in turn is one of the effects of planetary perturbations on the Earth. Laplace's initial computation accounted for the whole effect, thus seeming to tie up the theory neatly with both modern and ancient observations. However, in 1853, J C Adams caused the question to be re-opened by finding an error in Laplace's computations: it turned out that only about half of the Moon's apparent acceleration could be accounted for on Laplace's basis by the change in the Earth's orbital eccentricity.[27] (Adams showed that Laplace had in effect only considered the radial force on the moon and not the tangential, and the partial result hence had overstimated the acceleration, the remaining (negative), terms when accounted for, showed that Laplace's cause could not explain more than about half of the acceleration. The other half was subsequently shown to be due to tidal acceleration.[28])

Laplace used his results concerning the lunar acceleration when completing his attempted "proof" of the stability of the whole solar system on the assumption that it consists of a collection of rigid bodies moving in a vacuum.[6]

All the memoirs above alluded to were presented to the Académie des sciences, and they are printed in the Mémoires présentés par divers savants.[6]

Celestial mechanics

Classical mechanics
\mathbf{F} = m \mathbf{a}
History of classical mechanics · Timeline of classical mechanics
Scientists
Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson

Laplace now set himself the task to write a work which should "offer a complete solution of the great mechanical problem presented by the solar system, and bring theory to coincide so closely with observation that empirical equations should no longer find a place in astronomical tables." The result is embodied in the Exposition du système du monde and the Mécanique céleste.[6]

The former was published in 1796, and gives a general explanation of the phenomena, but omits all details. It contains a summary of the history of astronomy. This summary procured for its author the honour of admission to the forty of the French Academy and is commonly esteemed one of the masterpieces of French literature, though it is not altogether reliable for the later periods of which it treats.[6]

Laplace developed the nebular hypothesis of the formation of the solar system, first suggested by Emanuel Swedenborg and expanded by Immanuel Kant, a hypothesis that continues to dominate accounts of the origin of planetary systems. According to Laplace's description of the hypothesis, the solar system had evolved from a globular mass of incandescent gas rotating around an axis through its centre of mass. As it cooled, this mass contracted, and successive rings broke off from its outer edge. These rings in their turn cooled, and finally condensed into the planets, while the sun represented the central core which was still left. On this view, Laplace predicted that the more distant planets would be older than those nearer the sun.[6][29]

As mentioned, the idea of the nebular hypothesis had been outlined by Immanuel Kant in 1755,[29] and he had also suggested "meteoric aggregations" and tidal friction as causes affecting the formation of the solar system. Laplace was probably aware of this, but, like many writers of his time, he generally did not reference the work of others.[3]

Laplace's analytical discussion of the solar system is given in his Méchanique céleste published in five volumes. The first two volumes, published in 1799, contain methods for calculating the motions of the planets, determining their figures, and resolving tidal problems. The third and fourth volumes, published in 1802 and 1805, contain applications of these methods, and several astronomical tables. The fifth volume, published in 1825, is mainly historical, but it gives as appendices the results of Laplace's latest researches. Laplace's own investigations embodied in it are so numerous and valuable that it is regrettable to have to add that many results are appropriated from other writers with scanty or no acknowledgement, and the conclusions – which have been described as the organized result of a century of patient toil – are frequently mentioned as if they were due to Laplace.[6]

Jean-Baptiste Biot, who assisted Laplace in revising it for the press, says that Laplace himself was frequently unable to recover the details in the chain of reasoning, and, if satisfied that the conclusions were correct, he was content to insert the constantly recurring formula, "Il est aisé à voir que..." ("It is easy to see that..."). The Mécanique céleste is not only the translation of Newton's Principia into the language of the differential calculus, but it completes parts of which Newton had been unable to fill in the details. The work was carried forward in a more finely tuned form in Félix Tisserand's Traité de mécanique céleste (1889–1896), but Laplace's treatise will always remain a standard authority.[6]

Arcueil

Main article: Society of Arcueil

In 1806, Laplace bought a house in Arcueil, then a village and not yet absorbed into the Paris conurbation. Claude Louis Berthollet was a near neighbour and the pair formed the nucleus of an informal scientific circle, latterly known as the Society of Arcueil. Because of their closeness to Napoleon, Laplace and Berthollet effectively controlled advancement in the scientific establishment and admission to the more prestigious offices. The Society built up a complex pyramid of patronage.[30] In 1806, he was also elected a foreign member of the Royal Swedish Academy of Sciences.

Napoleon

An account of a famous interaction between Laplace and Napoleon is provided by Rouse Ball:[6]

Laplace went in state to Napoleon to present a copy of his work, and the following account of the interview is well authenticated, and so characteristic of all the parties concerned that I quote it in full. Someone had told Napoleon that the book contained no mention of the name of God; Napoleon, who was fond of putting embarrassing questions, received it with the remark, 'M. Laplace, they tell me you have written this large book on the system of the universe, and have never even mentioned its Creator.' Laplace, who, though the most supple of politicians, was as stiff as a martyr on every point of his philosophy, drew himself up and answered bluntly, Je n'avais pas besoin de cette hypothèse-là. ("I had no need of that hypothesis.") Napoleon, greatly amused, told this reply to Lagrange, who exclaimed, Ah! c'est une belle hypothèse; ça explique beaucoup de choses. ("Ah, it is a fine hypothesis; it explains many things.")

Black holes

Laplace also came close to propounding the concept of the black hole. He pointed out that there could be massive stars whose gravity is so great that not even light could escape from their surface (see escape velocity).[31] Laplace also speculated that some of the nebulae revealed by telescopes may not be part of the Milky Way and might actually be galaxies themselves. Thus, he anticipated Edwin Hubble's major discovery 100 years in advance.

Analytic theory of probabilities

In 1812, Laplace issued his Théorie analytique des probabilités in which he laid down many fundamental results in statistics. In 1819, he published a popular account of his work on probability. This book bears the same relation to the Théorie des probabilités that the Système du monde does to the Méchanique céleste.[6]

Probability-generating function

The method of estimating the ratio of the number of favourable cases to the whole number of possible cases, had been previously indicated by Laplace in a paper written in 1779. It consists of treating the successive values of any function as the coefficients in the expansion of another function, with reference to a different variable. The latter is therefore called the probability-generating function of the former. Laplace then shows how, by means of interpolation, these coefficients may be determined from the generating function. Next he attacks the converse problem, and from the coefficients he finds the generating function; this is effected by the solution of a finite difference equation.[6]

Least squares

This treatise includes an exposition of the method of least squares, a remarkable testimony to Laplace's command over the processes of analysis. The method of least squares for the combination of numerous observations had been given empirically by Carl Friedrich Gauss (around 1794) and Legendre (in 1805), but the fourth chapter of this work contains a formal proof of it, on which the whole of the theory of errors has been since based. This was effected only by a most intricate analysis specially invented for the purpose, but the form in which it is presented is so meagre and unsatisfactory that, in spite of the uniform accuracy of the results, it was at one time questioned whether Laplace had actually gone through the difficult work he so briefly and often incorrectly indicates.[6]

Inductive probability

While he conducted much research in physics, another major theme of his life's endeavours was probability theory. In his Essai philosophique sur les probabilités (1814), Laplace set out a mathematical system of inductive reasoning based on probability, which we would today recognise as Bayesian. He begins the text with a series of principles of probability, the first six being:

1) Probability is the ratio of the "favored events" to the total possible events.

2) The first principle assumes equal probabilities for all events. When this is not true, we must first determine the probabilities of each event. Then, the probability is the sum of the probabilities of all possible favored events.

3) For independent events, the probability of the occurrence of all is the probability of each multiplied together.

4) For events not independent, the probability of event B following event A (or event A causing B) is the probability of A multiplied by the probability that A and B both occur.

5) The probability that A will occur, given B has occurred, is the probability of A and B occurring divided by the probability of B.

6) Three corollaries are given for the sixth principle, which amount to Bayesian probability. Where event Ai ∈ {A1, A2, ...An} exhausts the list of possible causes for event B, Pr(B) = Pr(A1, A2, ...An). Then

\Pr(A_i |B) = \frac{\Pr(B|A_i)}{\sum_{i}\Pr(B|A_i)}.

One well-known formula arising from his system is the rule of succession, given as principle seven. Suppose that some trial has only two possible outcomes, labeled "success" and "failure". Under the assumption that little or nothing is known a priori about the relative plausibilities of the outcomes, Laplace derived a formula for the probability that the next trial will be a success.

\Pr(\text{next outcome is success}) = \frac{s%2B1}{n%2B2}

where s is the number of previously observed successes and n is the total number of observed trials. It is still used as an estimator for the probability of an event if we know the event space, but only have a small number of samples.

The rule of succession has been subject to much criticism, partly due to the example which Laplace chose to illustrate it. He calculated that the probability that the sun will rise tomorrow, given that it has never failed to in the past, was

\Pr(\text{sun will rise tomorrow}) = \frac{d%2B1}{d%2B2}

where d is the number of times the sun has risen in the past. This result has been derided as absurd, and some authors have concluded that all applications of the Rule of Succession are absurd by extension. However, Laplace was fully aware of the absurdity of the result; immediately following the example, he wrote, "But this number [i.e., the probability that the sun will rise tomorrow] is far greater for him who, seeing in the totality of phenomena the principle regulating the days and seasons, realizes that nothing at the present moment can arrest the course of it."[32]

Laplace's demon

Main article: Laplace's demon

Laplace published the first articulation of causal or scientific determinism:[33]

We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.
—Pierre Simon Laplace, A Philosophical Essay on Probabilities[34]

This intellect is often referred to as Laplace's demon (in the same vein as Maxwell's demon) and sometimes Laplace's Superman (after Hans Reichenbach). Laplace, himself, did not use the word "demon", which was a later embellishment. As translated into English above, he simply referred to: "Une intelligence... Rien ne serait incertain pour elle, et l'avenir comme le passé, serait présent à ses yeux."

Laplace transforms

Main article: Laplace transform#History

As early as 1744, Euler, followed by Lagrange, had started looking for solutions of differential equations in the form:[35]

z = \int X(x) e^{ax} \,dx\text{ and }z = \int X(x) x^a \,dx.

In 1785, Laplace took the key forward step in using integrals of this form in order to transform a whole difference equation, rather than simply as a form for the solution, and found that the transformed equation was easier to solve than the original.[36][37]

Other discoveries and accomplishments

Mathematics

Amongst the other discoveries of Laplace in pure and applicable mathematics are:

Surface tension

Main article: Young-Laplace equation#History

Laplace built upon the qualitative work of Thomas Young to develop the theory of capillary action and the Young-Laplace equation.

Speed of sound

Laplace in 1816 was the first to point out that the speed of sound in air depends on the heat capacity ratio. Newton's original theory gave too low a value, because it does not take account of the adiabatic compression of the air which results in a local rise in temperature and pressure. Laplace's investigations in practical physics were confined to those carried on by him jointly with Lavoisier in the years 1782 to 1784 on the specific heat of various bodies.[6]

Political ambitions

According to W. W. Rouse Ball, as Napoleon's power increased Laplace begged him to give him the post of Minister of the Interior. However this is disputed by Pearson.[3] Napoleon, who desired the support of men of science, did make him Minister of the Interior in November 1799, but a little less than six weeks saw the close of Laplace's political career. Napoleon later (in his Mémoires de Sainte Hélène) wrote of his dismissal as follows:[6]

Géomètre de premier rang, Laplace ne tarda pas à se montrer administrateur plus que médiocre; dès son premier travail nous reconnûmes que nous nous étions trompé. Laplace ne saisissait aucune question sous son véritable point de vue: il cherchait des subtilités partout, n'avait que des idées problématiques, et portait enfin l'esprit des `infiniment petits' jusque dans l'administration. (Geometrician of the first rank, Laplace was not long in showing himself a worse than average administrator; since his first actions in office we recognized our mistake. Laplace did not consider any question from the right angle: he sought subtleties everywhere, only conceived problems, and finally carried the spirit of "infinitesimals" into the administration.)

Lucien, Napoleon's brother, was given the post. Although Laplace was removed from office, it was desirable to retain his allegiance. He was accordingly raised to the senate, and to the third volume of the Mécanique céleste he prefixed a note that of all the truths therein contained the most precious to the author was the declaration he thus made of his devotion towards the peacemaker of Europe. In copies sold after the Bourbon Restoration this was struck out. (Pearson points out that the censor would not have allowed it anyway.) In 1814 it was evident that the empire was falling; Laplace hastened to tender his services to the Bourbons, and in 1817 during the Restoration he was rewarded with the title of marquis.

According to Rouse Ball, the contempt that his more honest colleagues felt for his conduct in the matter may be read in the pages of Paul Louis Courier. His knowledge was useful on the numerous scientific commissions on which he served, and probably accounts for the manner in which his political insincerity was overlooked.[6]

He died in Paris in 1827. His brain was removed by his physician, François Magendie, and kept for many years, eventually being displayed in a roving anatomical museum in Britain. It was reportedly smaller than the average brain.[3]

Honours

Quotes

References

  1. ^ Stephen M. Stigler (1986) The history of statistics. Harvard University press. Chapter 3.
  2. ^ [Anon.] (1911) "Pierre Simon, Marquis De Laplace", Encyclopaedia Britannica
  3. ^ a b c d e f g "Laplace, being Extracts from Lectures delivered by Karl Pearson", Biometrika, vol. 21, Dec. 1929, pp. 202–16
  4. ^ a b *O'Connor, John J.; Robertson, Edmund F., "Pierre-Simon Laplace", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Laplace.html ., accessed 25 August 2007
  5. ^ Gillispie (1997) pp3–4
  6. ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad Rouse Ball (1908)
  7. ^ Gillispie (1997) pp5
  8. ^  "Pierre-Simon Laplace". Catholic Encyclopedia. New York: Robert Appleton Company. 1913. 
  9. ^ Gillispie (1989) pp7–12
  10. ^ Gillispie (1989) pp14–15
  11. ^ a b Whitrow (2001)
  12. ^ Celletti, A. & Perozzi, E. (2007). Celestial Mechanics: The Waltz of the Planets. Berlin: Springer. pp. 91–93. ISBN 0-387-30777-X. 
  13. ^ Whittaker (1949b)
  14. ^ Gillispie (1989) pp29–35
  15. ^ Gillispie (1989) pp35–36
  16. ^ School of Mathematics and Statistics, University of St Andrews, Scotland.
  17. ^ Grattan-Guinness, I. (2003). Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Baltimore: Johns Hopkins University Press. pp. 1097–1098. ISBN 0801873967. http://books.google.com/?id=f5FqsDPVQ2MC&pg=PA1098&lpg=PA1098&dq=laplace+potential+1784. 
  18. ^ W. W. Rouse Ball A Short Account of the History of Mathematics (4th edition, 1908)
  19. ^ Green, G. (1828). An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism. Nottingham. arXiv:0807.0088. 
  20. ^ Kline, Morris (1972). Mathematical thought from ancient to modern times, Volume 2. Oxford University Press. pp. 524–525. ISBN 0-19-506136-5. 
  21. ^ Euler, Leonard (1756/57). "General principles of the motion of fluids". Novi. Comm. Acad. Sci. Petrop.: 271–311. 
  22. ^ E Halley (1695), "Some Account of the Ancient State of the City of Palmyra, with Short Remarks upon the Inscriptions Found there", Phil. Trans., vol.19 (1695-1697), pages 160-175; esp. at pages 174-175.
  23. ^ Richard Dunthorne (1749), "A Letter from the Rev. Mr. Richard Dunthorne to the Reverend Mr. Richard Mason F. R. S. and Keeper of the Wood-Wardian Museum at Cambridge, concerning the Acceleration of the Moon", Philosophical Transactions (1683-1775), Vol. 46 (1749 - 1750) #492, pp.162-172; also given in Philosophical Transactions (abridgements) (1809), vol.9 (for 1744-49), p669-675 as "On the Acceleration of the Moon, by the Rev. Richard Dunthorne".
  24. ^ J de Lalande (1786): "Sur les equations seculaires du soleil et de la lune", Memoires de l'Academie Royale des Sciences, pp.390-397, at page 395.
  25. ^ J D North (2008), "Cosmos: an illustrated history of astronomy and cosmology", (University of Chicago Press, 2008), chapter 14, at page 454.
  26. ^ See also P Puiseux (1879), "Sur l'acceleration seculaire du mouvement de la Lune", Annales Scientifiques de l'Ecole Normale Superieure, 2nd series vol.8 (1879), pp.361-444, at pages 361-5.
  27. ^ J C Adams (1853), "On the Secular Variation of the Moon's Mean Motion", in Phil. Trans. R. Soc. Lond., vol.143 (1853), pages 397-406.
  28. ^ Roy, A. E. (2005). Orbital Motion. London: CRC Press. pp. 313. ISBN 0750310154. http://books.google.com/?id=Hzv7k2vH6PgC&pg=PA313&lpg=PA313&dq=laplace+secular+acceleration. 
  29. ^ a b Owen, T. C. (2001) "Solar system: origin of the solar system", Encyclopaedia Britannica, Deluxe CDROM edition
  30. ^ Crosland (1967) p.1
  31. ^ See Israel (1987), sec. 7.2.
  32. ^ Laplace, Pierre Simon, A Philosophical Essay on Probabilities, translated from the 6th French edition by Frederick Wilson Truscott and Frederick Lincoln Emory, Dover Publications (New York, 1951)
  33. ^ Hawking, Stephen. "Does God Play Dice?". Public Lectures. Archived from the original on 8 July 2000. http://web.archive.org/web/20000708041816/http://www.hawking.org.uk/lectures/dice.html. 
  34. ^ a b Laplace, Pierre Simon, A Philosophical Essay on Probabilities, translated from the 6th French edition by Frederick Wilson Truscott and Frederick Lincoln Emory, Dover Publications (New York, 1951) pp.4
  35. ^ Grattan-Guiness, in Gillispie (1997) p.260
  36. ^ Grattan-Guiness, in Gillispie (1997) pp261–262
  37. ^ Deakin (1981)
  38. ^ Schmadel, L. D. (2003). Dictionary of Minor Planet Names (5th rev. ed.). Berlin: Springer-Verlag. ISBN 3540002383. 
  39. ^ A sense of place in the heartland, The Milwaukee Journal Sentinel Online

Bibliography

By Laplace

English translations

About Laplace and his work

External links

Political offices
Preceded by
Nicolas Marie Quinette		 Minister of the Interior
12 November 1799 – 25 December 1799		 Succeeded by
Lucien Bonaparte
Cultural offices
Preceded by
Michel-Louis-Étienne Regnaud de Saint-Jean d'Angély		 Seat 8
Académie française
1816–1827		 Succeeded by
Pierre-Paul Royer-Collard